Mathe ist verrückt. Während die Grundlagen ziemlich einfach sind, kann die Philosophie hinter einigen dieser sehr einfachen Grundlagen ziemlich tiefgründig ... und sogar verwirrend sein. Heute werden wir alles von Primzahlen bis zur Unendlichkeit betrachten. Also mach dich bereit, denn das sind 25 außergewöhnliche mathematische Prinzipien, um dein Gehirn herauszufordern!
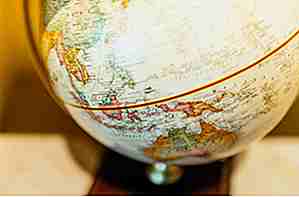
Das Äquatorseil
 Quelle: abc.net.au, Bild: pexels (public domain)
Quelle: abc.net.au, Bild: pexels (public domain) Wenn Sie ein Seil um den Äquator der Erde wickelten, so dass es sich eng an den Boden anschmiegt, müssten Sie nur etwa 6, 3 Meter Seil hinzufügen, damit das ganze Ding 1 Meter über dem Boden schwebt (rund um den Erde). Dieses nicht intuitive Ergebnis funktioniert unabhängig von der Größe der Kugel. Der einfachste Weg, dies zu erklären, besteht darin, sich daran zu erinnern, dass der Umfang gleich dem Durchmesser mal pi ist. Wenn Sie also das Seil 1 Meter über der Erde schweben lassen möchten, müssen Sie den Durchmesser nur um 2 Meter erhöhen (1 Meter an jedem Ende des Globus). Daher müssten Sie den Umfang des Seils nur um 2 x pi Meter (6.28318530718 Meter) vergrößern.
Hippasus von Metapontum
 Quelle: esoterx.com, Bild: https://commons.wikimedia.org (public domain)
Quelle: esoterx.com, Bild: https://commons.wikimedia.org (public domain) Der Mann, der bewiesen hat, dass irrationale Zahlen existieren, wurde dafür ermordet. Sein Name war Hippasus von Metapontum, und es geschah um 520 v. Pythagoras und viele griechische Mathematiker jener Zeit glaubten, dass alle Zahlen ganze Zahlen oder ganze Zahlen seien. Als Pythagoras seine berühmten Dreiecksberechnungen durchführte (Pythagoras Theorem), stolperte er über die Quadratwurzel von zwei. Um es kurz zu machen, er hat angeblich versucht, seine Entdeckung geheim zu halten, und hat es gekippt, als Hippasus es veröffentlicht hat.
Münchhausen-Nummern
 Quelle: zach.se
Quelle: zach.se Abgesehen von einigen Annahmen über 0 ^ 0, ist 3435 die einzige Zahl außer 1, in der Sie jede Ziffer aufteilen, auf ihre eigene Stärke erhöhen, alles zusammensummieren und die gleiche Zahl zurückbekommen können. Grundsätzlich gilt: 3 ^ 3 + 4 ^ 4 + 3 ^ 3 + 5 ^ 5 = 3435 Hinweis: 438579088 funktioniert auch, wenn Sie annehmen, dass 0 ^ 0 = 0 ist. Diese Zahlen werden Münchhausen-Nummern genannt.
Die Dezimaldarstellung der 7.s
 Bild: https://pixabay.com (public domain)
Bild: https://pixabay.com (public domain) Die Dezimaldarstellungen der 7ten sind die gleichen Zahlen, die wiederholt werden, außer dass sie immer von einem anderen Punkt ausgehen. 1/7 = 0.142857142857 ... und 2/7 = 0.285714285714 ... und 3/7 = 0.428571428571 ...
Binäre Fingerzählung
 Quelle: mathisfun.com, Bild: https://pixabay.com (public domain)
Quelle: mathisfun.com, Bild: https://pixabay.com (public domain) Wenn Sie binär verwenden, können Sie bis 1023 an Ihren Fingern zählen.
10!
 Quelle: reddit.com
Quelle: reddit.com Es sind genau 10! Sekunden in 6 Wochen. Es ist einfacher, dies zu sehen, wenn Sie es als solches abbrechen: 6 * 7 * 24 * 60 * 60 = 6 * 7 * (8 * 3) * (3 * 2 * 10) * (1 * 3 * 4 * 5) = 6 * 7 * 8 * 9 * 2 * 10 * 1 * 3 * 4 * 5 = 10!
Grahams Nummer
 Quelle: ibmathresources.com, Bild: https://pixabay.com (public domain)
Quelle: ibmathresources.com, Bild: https://pixabay.com (public domain) Grahams Zahl ist so groß, dass, wenn Sie jede Ziffer so klein wie möglich schreiben würden, sie immer noch mehr Platz beanspruchen würde, als im beobachtbaren Universum verfügbar ist. In der Tat, wenn Sie alle Ziffern in Ihrem Kopf halten könnten, würde Ihr Gehirn in ein schwarzes Loch kollabieren (aufgrund der astronomischen Dichte von neuronalen Verbindungen, die Sie benötigen würden).
Dezimale wiederholen
 Bild: https://pixabay.com (public domain)
Bild: https://pixabay.com (public domain) Jede sich wiederholende Dezimalzahl kann als Bruch über eine entsprechende Anzahl von 9 (als sich wiederholender Teil) geschrieben werden. Zum Beispiel wäre .456456456 ... 456/999
Karten mischen
 Quelle: qi.com, Bild: https://www.pexels.com (public domain)
Quelle: qi.com, Bild: https://www.pexels.com (public domain) Jedes Mal, wenn Sie ein Kartenspiel mit 52 Karten zufällig mischen, haben Sie es fast sicher in einer einzigartigen Reihenfolge angeordnet. Damit meinen wir, dass in der gesamten Geschichte der Menschheit noch nie jemand ein Deck auf dieselbe Weise gemischt hat. Wie? Nun, da sind 52! Möglichkeiten, das Deck zu bestellen (52 * 51 * 50 ...) Dies führt zu 8.0658 x 10 ^ 67 Möglichkeiten. Im Vergleich dazu ist das Universum nur 1 x 10 ^ 18 Sekunden alt. Selbst wenn du jede Sekunde seit dem Urknall ein Deck mischst ... du würdest immer noch kläglich knapp werden.
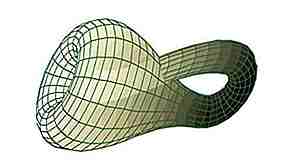
Die Klein-Flasche
 Quelle: math.union.edu
Quelle: math.union.edu Wenn Sie zwei Möbius-Streifen nehmen und die Kanten so verlängern, dass sie miteinander verbunden sind (und sie dadurch verkleben), erstellen Sie eine Klein-Flasche. Diese "Flasche" ist ein Beispiel einer nicht orientierbaren Oberfläche. Grundsätzlich existiert es nur in 4 Dimensionen, kann aber in 3 locker dargestellt werden. Wie der Möbius-Streifen hat er nur 1 Fläche, aber keine Kanten. Es ist ziemlich trippy.
Der frivole Satz der Arithmetik
 Quelle: mathworld.wolfram.com, Bild: https://pixabay.com (public domain)
Quelle: mathworld.wolfram.com, Bild: https://pixabay.com (public domain) Der frivole Satz der Arithmetik besagt, dass die überwiegende Mehrheit der natürlichen Zahlen aufgrund ihrer Unendlichkeit sehr, sehr groß ist.
Was liegt zwischen 0 und 1?

Es gibt unendlich viele Zahlen zwischen 0 und 1 (und 1 und 2 usw.). Zum Beispiel, ½, ⅓, ¼, und Sie können einfach weitermachen.
Nicht berechenbare Zahlen
 Quelle: igoro.com, Bild: http://www.pixnio.com (public domain)
Quelle: igoro.com, Bild: http://www.pixnio.com (public domain) Fast alle reellen Zahlen sind irrational. Mehr noch, die meisten irrationalen Zahlen sind nicht einmal berechenbar. Und um Ihre Gedanken wirklich zu verwirren, ist jede einzelne Zahl, die Sie jemals in Ihrem Leben gesehen haben, berechenbar, einschließlich unendlich wiederholter Zahlen wie pi (weil Sie einen Algorithmus erstellen können, um es zu berechnen). Also, um es einfach auszudrücken, es gibt eine unendliche Anzahl von Zahlen da draußen, die wir niemals sehen werden (in der Tat ... die meisten von ihnen), weil wir keine Möglichkeit haben, diese Zahlen zu berechnen. In gewisser Hinsicht sind sie die "dunkle Materie" der Mathematik. Wir wissen, dass sie da sind und dass sie die unsägliche Mehrheit der Zahlen bilden, aber wir haben keine Möglichkeit, sie zu erreichen. Anmerkung: Chaitins Konstante ist ein Beispiel für eine nicht-berechenbare Zahl, aber leider ... ist es nicht berechenbar.
Die verschiedenen Arten von Unendlichkeit
 Quelle: math.brown.edu, Bild: https://pixabay.com (public domain)
Quelle: math.brown.edu, Bild: https://pixabay.com (public domain) Obwohl die ganzen Zahlen unendlich sind, gibt es unendlich mehr reelle Zahlen als ganze Zahlen. Wie kann das sein, wenn die ganzen Zahlen bereits unendlich sind? Das liegt daran, dass es zwei Arten von Unendlichkeit gibt ... zählbar und unzählbar. Ganzzahlen sind unendlich zählbar, während reelle Zahlen nicht zählen (weil sie auch die irrationalen Zahlen enthalten). Das führt zu einigen verrückten Schlüssen. Die Anzahl der positiven ganzen Zahlen (0, 1, 2, ...) ist genau die gleiche wie die Anzahl der positiven und negativen ganzen Zahlen kombiniert (..., -3, -2, -1, 0, 1, 2, 3, ...). Obwohl diese beiden unendlichen Mengen gleich sind, sind sie beide kleiner als die unendliche Menge reeller Zahlen. Tatsächlich gibt es unendlich mehr Zahlen zwischen nur zwei zufälligen ganzen Zahlen (0 und 1 zum Beispiel) als es in der ganzen unendlichen Menge von ganzen Zahlen gibt!
Die normalen Nummern
 Quelle: mathworld.wolfram.com
Quelle: mathworld.wolfram.com Eine normale Zahl ist im Grunde eine irrationale Zahl, die keine Ziffer mehr hat als eine andere. So sollte zum Beispiel in der Nummer 4.56856948576434 ... jede einzelne Ziffer ungefähr gleich oft in der Unendlichkeit erscheinen. Obwohl es einen groben Beweis dafür gibt, dass die meisten reellen Zahlen normal sind, und wir vermuten, dass Zahlen wie pi und e normal sind, konnten wir es immer noch nicht zeigen.
Die Transzendentalen Zahlen
 Quelle: mathworld.wolfram.com
Quelle: mathworld.wolfram.com Obwohl fast jede einzelne reelle und komplexe Zahl transzendental ist (im Gegensatz zu algebraisch, was im Grunde jede Zahl ist, die die Wurzel eines Polynoms ist), gibt es nur wenige, die bekannt sind, hauptsächlich weil es wirklich schwierig ist, eine Zahl zu beweisen ist transzendental. Die bekanntesten transzendentalen Zahlen sind e und pi.
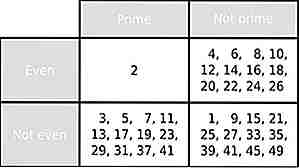
Die einsame Blüte
 Quelle: mathworld.wolfram.com, Bild: https://commons.wikimedia.org (public domain)
Quelle: mathworld.wolfram.com, Bild: https://commons.wikimedia.org (public domain) Jede einzelne Primzahl bis unendlich ist seltsam. Außer 2.
Der Effekt der Unendlichkeit auf die Wahrscheinlichkeit
 Bild: https://pixabay.com (public domain)
Bild: https://pixabay.com (public domain) Das Konzept der Unendlichkeit hat einige verrückte Auswirkungen auf die Wahrscheinlichkeit. Wählt man zufällig eine reelle Zahl, so ist die Wahrscheinlichkeit, dass sie rational ist (1, 2, ¾, 78/56, ...) 0. Dies geht auf die Tatsache zurück, dass die irrationalen Zahlen unendlich unendlich sind, während die rationalen Zahlen sind abzählbar unendlich. Und die zählbare Unendlichkeit über unzählige Unendlichkeiten ist 0.
.999 ... = 1
 Bild: https://commons.wikimedia.org (öffentliche Domäne)
Bild: https://commons.wikimedia.org (öffentliche Domäne) .999 ... ist gleich 1. An diesem Punkt ist Ihr Verstand wahrscheinlich so mit dem Konzept der Unendlichkeit verblüfft, dass Sie wahrscheinlich einfach alles akzeptieren werden, was wir Ihnen sagen, aber wir werden es beweisen. Sie wissen, dass .333 ... gleich ⅓ ist und .666 ... gleich ⅔ ist. ⅓ + ⅔ = 1 und .333 ... + .666 ... = .999 .... Eine andere Denkweise ist, dass, wenn .999 ... nicht gleich 1 ist, es eine Zahl zwischen .999 ... und 1 geben müsste, die es dank dem Konzept der Unendlichkeit nicht gibt.
Die Dirichlet-Funktion
 Quelle: mathworld.wolfram.com
Quelle: mathworld.wolfram.com Nach der Dirichlet-Funktion gibt es zwischen zwei irrationalen Zahlen eine rationale Zahl. Der verrückte Teil? Es gibt unendlich mehr irrationale Zahlen als rationale Zahlen (wie wir bereits festgestellt haben). Also ... wie könnten alle zwei irrationalen Zahlen eine rationale Zahl zwischen ihnen haben? Sie würden erwarten, dass die rationalen Zahlen ausgehen. Aber die Unendlichkeit verhält sich nicht so, wie wir es erwarten.
Eulers Identität
 Quelle: mathworld.wolfram.com
Quelle: mathworld.wolfram.com Eulers Identität wird oft als Beispiel für mathematische Schönheit genannt. Es ist e ^ (pi * i) + 1 = 0. Es enthält 5 der grundlegendsten mathematischen Konstanten 0, 1, e, pi und i. Außerdem treten drei der arithmetischen Grundoperationen genau einmal auf: Addition, Multiplikation und Potenzierung. Benjamin Peirce, ein bekannter Mathematiker sagte einmal, nachdem er es in einem Vortrag bewiesen hatte: "Die Identität ist absolut paradox; wir können es nicht verstehen, und wir wissen nicht, was es bedeutet, aber wir haben es bewiesen, und deshalb wissen wir, dass es die Wahrheit sein muss. "
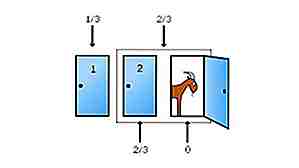
Das Monty Hall-Problem
 Quelle: mathworld.wolfram.com, Bild: https://commons.wikimedia.org (public domain)
Quelle: mathworld.wolfram.com, Bild: https://commons.wikimedia.org (public domain) Das Monty-Hall-Problem ist ein berühmtes Beispiel dafür, wie die Wahrscheinlichkeit kontraintuitiv sein kann. Nehmen wir an, dass es in einer Spielshow drei Türen gibt. Hinter einem von ihnen steht ein Auto, während die anderen zwei Ziegen verstecken. Sie wählen, Tür 1 zu öffnen. Der Wirt weiß jedoch, was hinter den Türen ist. Er öffnet Tür 3, um eine Ziege zu enthüllen. Jetzt fragt er Sie, ob Sie Ihre Wahl zu Tür 2 ändern möchten. Was machen Sie? Die Antwort ist, dass Sie Ihre Wahl ändern sollten. Warum? Denn wenn Sie zu Tür 2 wechseln, haben Sie eine Chance, das Auto zu gewinnen, während Sie an Tür 1 bleiben. Sie haben eine ungefähre Chance. Der beste Weg, diese nicht intuitive Lösung zu visualisieren, besteht darin, die Anzahl der Türen zu erhöhen. Sagen wir jetzt, dass es 100 Türen gibt. Du wählst Tür 37 aus. Der Wirt öffnet jetzt alle Türen, um Ziegen außer Tür 83 zu enthüllen. Möchtest du deine Auswahl von 37 auf 83 ändern? Oder würdest du auf 37 bleiben? Fakt ist, dass Ihre Chancen, das Auto zu gewinnen, durch den Wechsel zu Tür 83 erheblich steigen werden.
Der Unterschied zwischen 1 Million und 1 Milliarde

Eine Million Sekunden sind etwa 11 und ein halbes Tage. Eine Milliarde Sekunden sind knapp 32 Jahre.
Das Taubenschlag-Prinzip
 Quelle: mathworld.wolfram.com, Bild: https://commons.wikimedia.org (public domain)
Quelle: mathworld.wolfram.com, Bild: https://commons.wikimedia.org (public domain) Wenn Sie 2 Arten von Socken in Ihrer Schublade haben und Sie 3 zufällig ohne zu suchen greifen, haben Sie garantiert ein passendes Paar. Während dies für einige Menschen offensichtlich ist, kann es für andere schwerer zu verstehen sein. Es basiert auf etwas, das man das "Schublade-Prinzip" nennt. Grundsätzlich, wenn Sie n Arten von etwas haben, dann müssen Sie zufällig n + 1 des Dinges wählen, um eine Übereinstimmung zu erhalten. Also, wenn Sie 5 verschiedene Arten von Socken in Ihrer Schublade haben und Sie zufällig 6 von ihnen greifen ... Sie haben garantiert eine Übereinstimmung. Dies kann großartig sein, um sich im Dunkeln zu kleiden!
Die Summe aller positiven ganzen Zahlen von 1 bis unendlich
 Quelle: siehe unten, Bild: https://commons.wikimedia.org (public domain)
Quelle: siehe unten, Bild: https://commons.wikimedia.org (public domain) Nun, mach dich bereit für die vielleicht verrückteste Sache, die du jemals in deinem ganzen Leben hören wirst. Wenn Sie alle positiven ganzen Zahlen von 1 bis unendlich addieren ... was bekommen Sie? Hast du -1/12 erraten? Weil das die richtige Antwort ist. Wir wissen. Das hört sich absolut lächerlich an und ist teilweise so. Warum? Denn etwas bis ins Unendliche hinzuzufügen, ist unmöglich und führt zu lächerlichen Ergebnissen. Um das Ganze noch verrückter zu machen, ist dieses Ergebnis in der Physik, insbesondere der Stringtheorie, sehr gut bekannt. In der Tat, wenn Sie immer noch nicht glauben können, empfehlen wir Ihnen, dieses Video von den Physikern Tony Padilla und Ed Copeland von der University of Nottingham zu sehen. Sie erklären die Verrücktheit besser als wir - https://www.youtube.com/watch?v=w-I6XTVZXww.
Anmerkung: Das Ergebnis ergibt sich weitgehend aus der Tatsache, dass die Unendlichkeit unseren Erwartungen widerspricht. Infinity ist keine Nummer, es ist ein Konzept. Dinge wie Addition und Subtraktion funktionieren nicht gleich, wenn du die Unendlichkeit mit einbeziehst (eine Art, wie Physik nicht gleich funktioniert, wenn du in der Mitte eines Schwarzen Lochs stehst).
Weitere Informationen: Es lohnt sich auch Ramanujan Summation und Grandi's Serie zu betrachten:
https://en.wikipedia.org/wiki/Ramanujan_summation
https://en.wikipedia.org/wiki/Grandi's_series
Eine weitere Ressource:
http://www.bradyharanblog.com/blog/2015/1/11/this-blog-probably-wont-help
Fotos: Ausgewähltes Bild: https://commons.wikimedia.org (public domain), 20. max. Pixel, 16. Tttrung, Klein Flasche2, CC BY-SA 4.0, 11. Mehran Moghtadaei, PP 1280 × 1024, CC BY- SA 3.0, 10. Stephen J. Brooks (Vortrag), Algebraicszoom, CC BY 3.0, 6. Judy Breck via Flickr, CC BY-SA 2.0, 5. Quinn Dombrowski aus Chicago, USA, Eulers Identity Graffito, CC BY-SA 2.0, 3. Cmglee, Visualisierung 1 Milliarde, CC BY-SA 3.0,




