25 einfache geistige Mathetricks, die deinen Verstand durchbrennen

Um festzustellen, ob eine Zahl durch drei teilbar ist, addieren Sie die Ziffern. Wenn die Summe durch drei teilbar ist, ist auch die Zahl. Hinweis: Dies funktioniert auch für 9.

x% von y ist gleich wie y% von x. Das heißt, wenn 2% von 50 zu schwierig sind, können Sie es einfach umdrehen - 50% von 2. Das ist viel einfacher.

Um eine 2-stellige Zahl mit 11 zu multiplizieren, addieren Sie einfach die Ziffern zusammen und kleben Sie die Antwort dazwischen. Zum Beispiel wäre 42 * 11 4 + 2 = 6. Nun lege die 6 zwischen die 4 und die 2, um 462 zu erhalten.

Hinweis: Vergessen Sie nicht, die 1 zu tragen. Um ein anderes Beispiel zu geben, wäre 58 * 11 5 + 8 = 13. Sie können nicht einfach die 13 zwischen die 5 und die 8 setzen. Das würde 5138 ergeben, was offensichtlich falsch ist. Sie müssen den einen tragen, indem Sie ihn zum 5. hinzufügen. So wäre es 638.

Wenn Sie eine Zahl mit 5 multiplizieren müssen, kann es einfacher sein, sie zu halbieren und dann mit 10 zu multiplizieren. Beispiel: 315 * 5 wäre 315/2 = 157.5 Verschieben Sie jetzt einfach die Dezimalstelle, um mit 10 zu multiplizieren und 1575 zu erhalten.

Um eine Quadratwurzel zu approximieren, machen Sie folgendes. Finde das nächst niedrigere perfekte Quadrat. Fügen Sie es Ihrer Nummer hinzu. Jetzt dividiere durch die Quadratwurzel des unteren perfekten Quadrats. Und nun wieder durch 2 teilen. Klingt schwer? Hier ist ein Beispiel. Take 31. Das nächstniedrigste perfekte Quadrat ist 25. Also ist 31 plus 25 gleich 56. Nun dividiere durch die Quadratwurzel von 25. Also 56/5 = 11.2 Jetzt dividiere durch 2 um 5.6 zu erhalten

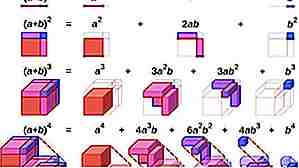
Verwenden Sie den Binomialsatz (a + b) ^ 2 = a ^ 2 + 2ab + b ^ 2 zu Quadratzahlen. Zum Beispiel könnte 55 ^ 2 (50 + 5) ^ 2 sein. Dies bedeutet, dass 50 * 50 + 50 * 5 * 2 + 5 * 5 = 2500 + 500 + 25 = 3025.

Um zu sehen, ob eine Zahl durch 8 teilbar ist, überprüfen Sie die letzten drei Ziffern. Wenn sie durch 8 teilbar sind, dann ist die Zahl durch 8 teilbar. Zum Beispiel wäre 3423024 durch 8 teilbar, weil 024/8 = 3 ist

Um einen Tipp zu ziehen, bewegen Sie die Dezimalstelle um eine Stelle nach links, um 10% zu erhalten. Dann addieren Sie entweder die Hälfte von dem, was Sie übrig haben, um 15% zu bekommen, oder verdoppeln Sie es um 20%. Zum Beispiel, wenn die Rechnung $ 43.21 ist, dann ist 4, 32 $ 10%. Die Hälfte von 4, 32 $ ist 2, 16 $. Wenn Sie also 15% wollen, fügen Sie das einfach hinzu. Es würde Ihnen $ 4, 32 + $ 2, 16 = $ 6, 48 geben. 20% zu bekommen ist noch einfacher, weil Sie es nur verdoppeln. 4, 32 $ * 2 = 8, 64 $. Wenn Sie sich also großzügig fühlen, dann würden 8, 64 $ ein Trinkgeld von 20% ausmachen.

Um Ihr Jahresgehalt zu berechnen, nehmen Sie einfach Ihren Stundenlohn, verdoppeln Sie ihn und fügen Sie 3 Nullen hinzu. Nehmen wir an, Sie verdienen $ 8 pro Stunde. Verdoppeln Sie einfach das für $ 16 und fügen Sie dann drei Nullen für $ 16.000 hinzu.

Um die Umrechnung zwischen Celsius und Fahrenheit näherungsweise zu berechnen, multiplizieren Sie einfach mit 2 und fügen Sie 30 hinzu (von C bis F). Tun Sie das Gegenteil, um von F nach C zu gehen (subtrahieren Sie 30 und dividieren Sie durch 2).

Um zu sehen, ob eine Zahl durch 4 teilbar ist, sehen Sie sich einfach die letzten zwei Ziffern an. Wenn sie durch 4 teilbar sind, dann ist die ganze Zahl durch 4 teilbar. Also wäre 23746316 durch 4 teilbar, weil 16 durch 4 teilbar ist.

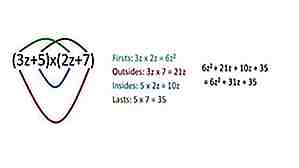
Um zwei Zahlen zu multiplizieren, verwenden Sie die FOIL-Methode (erste, äußere, innere, letzte). Zum Beispiel wäre 25 * 37 (20) (30) + (5) (30) + (7) (20) + (5) (7) = 925.

Hinweis: Dies ist genau das, was Sie tun, wenn Sie auf Papier multiplizieren, es ist einfach einfacher, die FOIL-Methode in Ihrem Kopf zu visualisieren.

Um den Prozentsatz einer Zahl (also nicht 10%) zu berechnen, suchen Sie zuerst 1% und multiplizieren Sie sie dann. So würden beispielsweise 3% von 528 528 * .01 = 5, 28 sein (die Dezimalstelle um zwei weitere Stellen verschieben). Jetzt multipliziere einfach mit 3, um 15, 84 zu erhalten

Dies funktioniert besonders gut, wenn eine der Zahlen bereits schön und rund ist (endet in 0). Einfach die andere Zahl abrunden, multiplizieren und das Ergebnis entsprechend anpassen. Zum Beispiel, wenn Sie 18 * 30 berechnen möchten, brauchen Sie nicht die FOIL-Methode, die wir früher gemacht haben (weil 30 bereits schön und rund ist). Mach einfach 20 * 30, was 600 ist und subtrahiere dann zwei 30s für 540.

Um zu überprüfen, ob eine Zahl durch 6 teilbar ist, müssen Sie zwei Teilbarkeitsregeln (zwei und drei) kombinieren. Wenn es sowohl durch 2 als auch durch 3 teilbar ist, dann ist es durch 6 teilbar. Wir haben die Teilbarkeit bereits durch 3 gemacht, aber nur für den Fall ... gerade Zahlen sind durch 2 teilbar.

Die Dezimaldarstellung der 11ten kann durch Multiplikation des Zählers mit 9 und nur Wiederholung erfolgen. Beispiel: 1/11 = .09090909 .... und 2/11 = .18181818 ... usw

Um eine zweistellige Zahl zu quadrieren, die auf 5 endet, setzen Sie einfach 25 am Ende und multiplizieren Sie die erste Zahl mit der folgenden Ziffer. So wäre zum Beispiel 45 ^ 2 2025, weil 5 die nächste Ziffer über 4 ist, also 4 * 5 = 20. Jetzt setze einfach eine 25 am Ende für 2025.

Die Dezimaldarstellungen für die Neunten sind nur der wiederholte Zähler. Zum Beispiel 1/9 = .1111111 ... und 2/9 = .2222222 ... Dies ist auch einer der Beweise, die verwendet werden, um zu zeigen, dass .999999 ... = 1. (seit 9/9 = .99999 ...)

Für die Quadrierung von Zahlen besteht ein möglicher Trick darin, von der Zahl zu addieren / subtrahieren, bis Sie zwei Zahlen erhalten, die Sie leicht multiplizieren können. Dann addiere die Differenz der Zahl, die du addiert / subtrahiert hast. Um ein Beispiel zu geben, könnte 46 ^ 2 42 * 50 sein, weil 46 - 4 = 42 und 46 + 4 = 50. Also 42 * 50 wäre 2100. Nun quadratisch die Zahl, die du addiert / subtrahiert hast, also 4 ^ 2 = 16. Jetzt füge 16 hinzu, um 2116 zu erhalten.

72 geteilt durch den Zinssatz geben Ihnen eine grobe Schätzung, wie viele Jahre es dauern würde, Ihr Geld zu verdoppeln (Regel 72).

Um geistig zu arbeiten, ist es viel einfacher, von links nach rechts zu arbeiten, als auf Papier (von rechts nach links). Dies liegt daran, dass Ihr Gehirn auf natürliche Weise Zahlen erkennt und erinnert, die auf der linken Seite beginnen. Zum Beispiel, um 376 + 581 zu machen, füge 300 + 500 hinzu, um 800 zu bekommen. Nun addiere 70 + 80, was 150 ist. Dies bringt die Summe auf 950. Dann addiere die 7 um 957 zu bekommen in kleinere Teile von links nach rechts. Ein weiterer Vorteil davon ist, dass Sie nach und nach auf die Lösung zugreifen. Wenn Sie also nur eine Annäherung wünschen, müssen Sie nicht warten, bis Sie das Problem gelöst haben, um herauszufinden, in welcher Größenordnung Sie arbeiten (Hunderte, Tausende usw.).

Für die mentale Subtraktion ähnelt die Idee der Addition. Arbeiten Sie von links nach rechts, aber es gibt einen zusätzlichen Trick, den Sie beachten müssen (Hinweis: Es beinhaltet Rundung). Nehmen wir an, Sie möchten 632 - 487 machen. Zuerst fügen Sie 3 hinzu, um 487 auf die nächsten 10 zu runden, also 490. Nun wird das Problem 632 - 490. Das ist viel einfacher. 632 - 400 ist 232. Nun subtrahieren Sie 90 und erhalten 142 (das sind 10 mehr als 100 subtrahieren). Denken Sie daran, die 3 von Anfang an hinzuzufügen. Das gibt dir 145.

Ein weiterer Trick zur Multiplikation von Zahlen, die leicht aufgerundet werden können (normalerweise mit 8 oder 9), ist die Verwendung der Subtraktionsmethode. Um dies zu tun, runden Sie die Zahl auf und subtrahieren Sie sie. Zum Beispiel wäre 49 * 16 50 * 16. Dies ist viel einfacher zu lösen. Da 100 * 16 ist 1600, können Sie die Hälfte, um 800 zu bekommen. Nun vergessen Sie nicht, zu subtrahieren, was Sie ursprünglich gerundet haben. Also, da du 49 bis 50 gerundet hast, war das 1 * 16, was du abziehen musst. Das ergibt 800 - 16, also 784.

Denken Sie daran, dass Sie alles tun können, was Sie für eine Gleichung tun möchten, solange Sie es auf beiden Seiten tun. Außerdem können Sie mit einem Begriff alles machen, was Sie wollen, solange Sie es mit einem multiplizieren. Denken Sie daran, dass 1 unendliche Formen hat (2/2, (x-4) / (x-4) usw.).

Um Meilen in Kilometer zu konvertieren, können Sie eine ziemlich genaue Schätzung erhalten, indem Sie 60% hinzufügen. Der schnellste Weg dazu besteht darin, 50% und dann 10% hinzuzufügen. Beispielsweise. 60 Meilen in km wären die folgenden: 60 * .5 = 30 und 60 * .1 = 6. Jetzt 30 + 6 = 36. Füge diese Zahl zu 60 hinzu, um 96 km zu erreichen. Um von Kilometer zu Meilen zu gehen, subtrahieren Sie 40%. Sie können dies tun, indem Sie 50% subtrahieren und dann 10% hinzufügen. Um also 350 km in Meilen zu erhalten, subtrahiere die Hälfte von 350. Das gibt dir 175. Nun füge wieder 10% von 350 hinzu, was 35 ist. Das lässt dich 210 zurück. Beachte: Das sind sehr grobe Schätzungen. Je größer Ihre Zahlen werden, desto mehr Fehler wird es geben.